নবম ও দশম শ্রেণীর অংক সমাধান ২০২৪-২৫ (অধ্যায়ঃ ১৬.২ চতুর্ভুজের ক্ষেত্রফল)

চতুর্ভুজের ক্ষেত্রফল:

১. একটি আয়তক্ষেত্রের দৈর্ঘ্য বিস্তারের দ্বিগুণ। এর ক্ষেত্রফল 512 বর্গমিটার হলে, পরিসীমা নির্ণয় কর।

দেওয়া আছে:

• আয়তক্ষেত্রের ক্ষেত্রফল = ৫১২ বর্গমিটার
• আয়তক্ষেত্রের দৈর্ঘ্য, প্রস্থের দ্বিগুণ।

মনে করি,

• আয়তক্ষেত্রের প্রস্থ = x মিটার
• আয়তক্ষেত্রের দৈর্ঘ্য = 2x মিটার

আমরা জানি, আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ

সুতরাং,

ক্ষেত্রফল = (2x) × x = 2x² বর্গমিটার

প্রশ্নানুসারে,

2x² = ৫১২

বা, x² = ৫১২/২

বা, x² = ২৫৬

বা, x = √২৫৬

বা, x = ১৬

অতএব,

• আয়তক্ষেত্রের প্রস্থ = ১৬ মিটার
• আয়তক্ষেত্রের দৈর্ঘ্য = ২ × ১৬ = ৩২ মিটার

আমরা জানি, আয়তক্ষেত্রের পরিসীমা = ২(দৈর্ঘ্য + প্রস্থ)

সুতরাং,

আয়তক্ষেত্রের পরিসীমা = ২(৩২ + ১৬)

= ২ × ৪৮

= ৯৬ মিটার

অতএব, আয়তক্ষেত্রটির পরিসীমা ৯৬ মিটার।

২. একটি জমির দৈর্ঘ্য 80 মিটার এবং প্রস্থ 60 মিটার। ঐ জমির মাঝে একটি পুকুর খনন করা হলো। যদি পুকুরের প্রত্যেক পাড়ের বিস্তার 4 মিটার হয়, তবে পুকুরের পাড়ের ক্ষেত্রফল নির্ণয় কর।

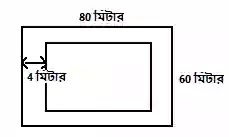
দেওয়া আছে:

• জমির দৈর্ঘ্য = ৮০ মিটার
• জমির প্রস্থ = ৬০ মিটার
• পাড়ের বিস্তার = ৪ মিটার (চারিদিকে)

সুতরাং,

• জমির ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ = ৮০ × ৬০ = ৪৮০০ বর্গমিটার

এখন, পাড় বাদে পুকুরের পরিমাপ বের করতে হবে। যেহেতু পাড়টি চারিদিকে ৪ মিটার করে বিস্তৃত, তাই দৈর্ঘ্য ও প্রস্থ উভয় দিক থেকেই ২ × ৪ = ৮ মিটার করে কমাতে হবে।

অতএব,

• পাড় বাদে পুকুরের দৈর্ঘ্য = ৮০ – (২ × ৪) = ৮০ – ৮ = ৭২ মিটার
• পাড় বাদে পুকুরের প্রস্থ = ৬০ – (২ × ৪) = ৬০ – ৮ = ৫২ মিটার

সুতরাং,

• পাড় বাদে পুকুরের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ = ৭২ × ৫২ = ৩৭৪৪ বর্গমিটার

অতএব, শুধুমাত্র পাড়ের ক্ষেত্রফল = জমির ক্ষেত্রফল – পাড় বাদে পুকুরের ক্ষেত্রফল

= ৪৮০০ বর্গমিটার – ৩৭৪৪ বর্গমিটার

= ১০৫৬ বর্গমিটার

সুতরাং, পাড়ের ক্ষেত্রফল ১০৫৬ বর্গমিটার।

৩. একটি বাগানের দৈর্ঘ্য 40 মিটার এবং পেস্থ 30 মিটার। বাগানের ভিতরে সমান পাড় বিশিষ্ট একটি পুকুর আছে। পুকুরের ক্ষেত্রফল বাগানের ক্ষেত্রফলের ½ অংশ হলে, পুকুরের দৈর্ঘ্য ও প্রস্থ নির্ণয় কর।

সমাধানঃ

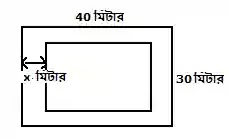
দেওয়া আছে:

• বাগানের দৈর্ঘ্য = ৪০ মিটার
• বাগানের প্রস্থ = ৩০ মিটার

সুতরাং,

• বাগানের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ = ৪০ × ৩০ = ১২০০ বর্গমিটার

মনে করি,

• পুকুরের পাড়ের বিস্তার = x মিটার

অতএব,

• পুকুরের দৈর্ঘ্য = ৪০ – ২x মিটার (যেহেতু পাড় উভয় দিকে x মিটার করে আছে)
• পুকুরের প্রস্থ = ৩০ – ২x মিটার (যেহেতু পাড় উভয় দিকে x মিটার করে আছে)

সুতরাং,

• পুকুরের ক্ষেত্রফল = (৪০ – ২x)(৩০ – ২x) বর্গমিটার

প্রশ্নানুসারে, পুকুরের ক্ষেত্রফল বাগানের ক্ষেত্রফলের অর্ধেক।

অতএব,

(৪০ – ২x)(৩০ – ২x) = (১/২) × ১২০০

বা, (৪০ – ২x)(৩০ – ২x) = ৬০০

বা, ১২০০ – ৮০x – ৬০x + ৪x² = ৬০০

বা, ৪x² – ১৪০x + ১২০০ – ৬০০ = ০

বা, ৪x² – ১৪০x + ৬০০ = ০

উভয় পক্ষকে ৪ দিয়ে ভাগ করে পাই:

বা, x² – ৩৫x + ১৫০ = ০

এখন, এই দ্বিঘাত সমীকরণটি সমাধান করি:

বা, x² – ৩০x – ৫x + ১৫০ = ০

বা, x(x – ৩০) – ৫(x – ৩০) = ০

বা, (x – ৫)(x – ৩০) = ০

অতএব, x – ৫ = ০ অথবা x – ৩০ = ০

সুতরাং, x = ৫ অথবা x = ৩০

যেহেতু বাগানের প্রস্থ ৩০ মিটার, তাই পুকুরের পাড়ের বিস্তার ৩০ মিটার হতে পারে না। তাই, x = ৩০ গ্রহণযোগ্য নয়।

অতএব, পুকুরের পাড়ের বিস্তার x = ৫ মিটার।

এখন, পুকুরের দৈর্ঘ্য ও প্রস্থ নির্ণয় করি:

• পুকুরের দৈর্ঘ্য = ৪০ – ২ × ৫ = ৪০ – ১০ = ৩০ মিটার
• পুকুরের প্রস্থ = ৩০ – ২ × ৫ = ৩০ – ১০ = ২০ মিটার

সুতরাং,

• পুকুরের দৈর্ঘ্য = ৩০ মিটার
• পুকুরের প্রস্থ = ২০ মিটার

৪. একটি বর্গাকার মাঠের বাইরে চারদিকে 5 মিটার চওড়া একটি রাস্তা আছে। রাস্তার ক্ষেত্রফল 500 বর্গমিটার হলে, মাঠের ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

মনে করি,

• বর্গাকার মাঠের এক বাহুর দৈর্ঘ্য = x মিটার

সুতরাং,

• মাঠের ক্ষেত্রফল = x² বর্গমিটার

দেওয়া আছে:

• রাস্তার ক্ষেত্রফল = ৫০০ বর্গমিটার

অতএব,

• রাস্তাসহ মাঠের ক্ষেত্রফল = x² + ৫০০ বর্গমিটার … (i)

আবার,

• রাস্তাসহ বর্গাকার মাঠের এক বাহুর দৈর্ঘ্য = x + (৫ + ৫) = x + ১০ মিটার (যেহেতু রাস্তাটি মাঠের চারিদিকে ৫ মিটার চওড়া)

সুতরাং,

• রাস্তাসহ বর্গাকার মাঠের ক্ষেত্রফল = (x + ১০)² বর্গমিটার … (ii)

(i) ও (ii) থেকে পাই:

x² + ৫০০ = (x + ১০)²

বা, x² + ৫০০ = x² + ২০x + ১০০

উভয় পক্ষ থেকে x² বিয়োগ করে পাই:

বা, ৫০০ = ২০x + ১০০

বা, ৫০০ – ১০০ = ২০x

বা, ৪০০ = ২০x

বা, x = ৪০০/২০

বা, x = ২০

অতএব,

• বর্গাকার মাঠের এক বাহুর দৈর্ঘ্য = ২০ মিটার

সুতরাং,

• মাঠের ক্ষেত্রফল = x² = ২০² = ৪০০ বর্গমিটার

অতএব, বর্গাকার মাঠের ক্ষেত্রফল ৪০০ বর্গমিটার।

৫. একটি বর্গক্ষেত্রের পরিসীমা একটি আয়তক্ষেত্রের পরিসীমার সমান। আয়তক্ষেত্রটির দৈর্ঘ্য প্রস্থের তিনগুণ এবং ক্ষেত্রফল 768 বর্গমিটার। প্রতিটি 40 সেমি বর্গাকার পাথর দিয়ে বর্গক্ষেত্রটি বাঁধতে মোট কতটি পাথর লাগবে?

সমাধানঃ

দেওয়া আছে:

• আয়তক্ষেত্রের দৈর্ঘ্য, প্রস্থের ৩ গুণ।
• আয়তক্ষেত্রের ক্ষেত্রফল = ৭৬৮ বর্গমিটার।

মনে করি,

• আয়তক্ষেত্রের প্রস্থ = x মিটার।
• আয়তক্ষেত্রের দৈর্ঘ্য = ৩x মিটার।

আমরা জানি, আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ।

সুতরাং,

ক্ষেত্রফল = (৩x) × x = ৩x² বর্গমিটার

প্রশ্নানুসারে,

৩x² = ৭৬৮

বা, x² = ৭৬৮/৩

বা, x² = ২৫৬

বা, x = √২৫৬

বা, x = ১৬

অতএব,

• আয়তক্ষেত্রের প্রস্থ = ১৬ মিটার।
• আয়তক্ষেত্রের দৈর্ঘ্য = ৩ × ১৬ = ৪৮ মিটার।

এখন, আয়তক্ষেত্রের পরিসীমা = ২(দৈর্ঘ্য + প্রস্থ)

= ২(৪৮ + ১৬)

= ২ × ৬৪

= ১২৮ মিটার।

প্রশ্নানুসারে, এই পরিসীমা একটি বর্গক্ষেত্রের পরিসীমার সমান।

মনে করি,

• বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য = a মিটার।

আমরা জানি, বর্গক্ষেত্রের পরিসীমা = ৪a

সুতরাং,

৪a = ১২৮

বা, a = ১২৮/৪

বা, a = ৩২ মিটার।

অতএব,

• বর্গক্ষেত্রের এক বাহুর দৈর্ঘ্য = ৩২ মিটার।

সুতরাং, বর্গক্ষেত্রের ক্ষেত্রফল = a² = ৩২² = ১০২৪ বর্গমিটার।

দেওয়া আছে,

• বর্গাকার প্রতিটি পাথরের দৈর্ঘ্য = ৪০ সেমি = ০.৪ মিটার (১০০ সেমি = ১ মিটার, তাই ৪০ সেমি = ৪০/১০০ = ০.৪ মিটার)

অতএব,

• বর্গাকার পাথরের ক্ষেত্রফল = (০.৪)² = ০.১৬ বর্গমিটার।

সুতরাং, বর্গক্ষেত্রটির জন্য পাথর লাগবে = বর্গক্ষেত্রের ক্ষেত্রফল / প্রতিটি পাথরের ক্ষেত্রফল

= ১০২৪ / ০.১৬

= ৬৪০০ টি।

অতএব, নির্ণেয় পাথরের সংখ্যা ৬৪০০ টি।

৬. একটি আয়তাকারক্ষেত্রের ক্ষেত্রফল 160 বর্গমিটার। যদি এর দৈর্ঘ্য 6 মিটার কম হয়, তবে ক্ষেত্রটি বর্গাকার হয়। আয়তাকারক্ষেত্রের দৈর্ঘ্য ও প্রস্থ নির্ণয় কর।

সমাধানঃ

মনে করি,

• আয়তক্ষেত্রের দৈর্ঘ্য = x মিটার
• আয়তক্ষেত্রের প্রস্থ = y মিটার

দেওয়া আছে:

• আয়তক্ষেত্রের ক্ষেত্রফল = ১৬০ বর্গমিটার

সুতরাং,

• x × y = xy = ১৬০ … (i)

আরও দেওয়া আছে:

• দৈর্ঘ্য, প্রস্থের থেকে ৬ মিটার বেশি।

সুতরাং,

• x = y + ৬ … (ii)

এখন, (ii) নং সমীকরণ থেকে x এর মান (i) নং সমীকরণে বসিয়ে পাই:

(y + ৬)y = ১৬০

বা, y² + ৬y = ১৬০

বা, y² + ৬y – ১৬০ = ০

এটি একটি দ্বিঘাত সমীকরণ। এটিকে উৎপাদকে বিশ্লেষণ করে সমাধান করা যায়:

y² + ১৬y – ১০y – ১৬০ = ০

বা, y(y + ১৬) – ১০(y + ১৬) = ০

বা, (y + ১৬)(y – ১০) = ০

অতএব, y + ১৬ = ০ অথবা y – ১০ = ০

সুতরাং, y = -১৬ অথবা y = ১০

যেহেতু প্রস্থ ঋণাত্মক হতে পারে না, তাই y = -১৬ গ্রহণযোগ্য নয়।

অতএব,

• আয়তক্ষেত্রের প্রস্থ (y) = ১০ মিটার

এখন, (ii) নং সমীকরণে y এর মান বসিয়ে x এর মান বের করি:

x = y + ৬ = ১০ + ৬ = ১৬

অতএব,

• আয়তক্ষেত্রের দৈর্ঘ্য (x) = ১৬ মিটার

সুতরাং, আয়তক্ষেত্রের প্রস্থ ১০ মিটার এবং দৈর্ঘ্য ১৬ মিটার।

৭. একটি সামন্তরিকের ভুমি উচ্চতার ¾ অংশ এবং ক্ষেত্রফল 363 বর্গমিটার হলে, ক্ষেত্রটির ভূমি ও উচ্চতা নির্ণয় কর।

সমাধানঃ

মনে করি,

• সামন্তরিকটির উচ্চতা = h মিটার

সুতরাং,

• সামন্তরিকটির ভূমি = (৩/৪)h মিটার

আমরা জানি, সামন্তরিকের ক্ষেত্রফল = ভূমি × উচ্চতা

সুতরাং,

সামন্তরিকের ক্ষেত্রফল = (৩/৪)h × h = (৩/৪)h² বর্গমিটার

প্রশ্নমতে,

সামন্তরিকের ক্ষেত্রফল = ৩৬৩ বর্গমিটার

অতএব,

(৩/৪)h² = ৩৬৩

বা, ৩h² = ৩৬৩ × ৪

বা, ৩h² = ১৪৫২

বা, h² = ১৪৫২/৩

বা, h² = ৪৮৪

বা, h = √৪৮৪

বা, h = ২২

অতএব,

• সামন্তরিকটির উচ্চতা = ২২ মিটার
• সামন্তরিকটির ভূমি = (৩/৪) × ২২ = ১৬.৫ মিটার

সুতরাং, সামন্তরিকটির উচ্চতা ২২ মিটার এবং ভূমি ১৬.৫ মিটার।

৮. একটি সামন্তরিকের ক্ষেত্রফল একটি বর্গক্ষেত্রের সমান। সামন্তরিকের ভূমি 125 মিটার এবং উচ্চতা 5 মিটার হলে, বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য নির্ণয় কর।

সমাধানঃ

আপনার সমাধানটি সম্পূর্ণ সঠিক। উপস্থাপনার সুবিধার জন্য এবং আরও স্পষ্ট করে বোঝানোর জন্য, নিচে একটি পুনর্লিখিত সমাধান দেওয়া হলো:

দেওয়া আছে:

• সামন্তরিকের ভূমি = ১২৫ মিটার
• সামন্তরিকের উচ্চতা = ৫ মিটার

সুতরাং,

• সামন্তরিকের ক্ষেত্রফল = ভূমি × উচ্চতা = ১২৫ × ৫ = ৬২৫ বর্গমিটার

শর্তানুসারে,

• বর্গের ক্ষেত্রফল = সামন্তরিকের ক্ষেত্রফল = ৬২৫ বর্গমিটার

মনে করি,

• বর্গের বাহুর দৈর্ঘ্য = a মিটার

আমরা জানি, বর্গের ক্ষেত্রফল = a²

সুতরাং,

a² = ৬২৫

বা, a = √৬২৫

বা, a = ২৫

অতএব,

• বর্গের বাহুর দৈর্ঘ্য = ২৫ মিটার

আমরা জানি, বর্গের কর্ণের দৈর্ঘ্য = a√২

সুতরাং,

বর্গের কর্ণের দৈর্ঘ্য = ২৫√২ ≈ ২৫ × ১.৪১৪ = ৩৫.৩৫ মিটার (প্রায়)

অথবা, আরও সঠিকভাবে √২ এর মান ১.৪১৪২১৩৬ ব্যবহার করলে,

বর্গের কর্ণের দৈর্ঘ্য = ২৫√২ ≈ ২৫ × ১.৪১৪২১৩৬ ≈ ৩৫.৩৬ মিটার (প্রায়)

অতএব, বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য প্রায় ৩৫.৩৬ মিটার।

৯. একটি সামন্তরিকের বাহুর দৈর্ঘ্য 30 সেমি এবং 26 সেমি। এর ক্ষুদ্রতম কর্ণটি 28 সেমি হলে অপর কর্ণের দৈর্ঘ্য নির্ণয় কর।

সমাধানঃ

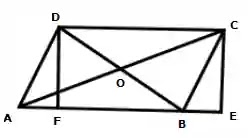
দেওয়া আছে:

• ABCD সামন্তরিকের AB = CD = ৩০ সেমি
• AD = BC = ২৬ সেমি
• ক্ষুদ্রতম কর্ণ BD = ২৮ সেমি

নির্ণয় করতে হবে: বৃহত্তম কর্ণ AC এর দৈর্ঘ্য।

অঙ্কন: D ও C থেকে AB এবং AB এর বর্ধিতাংশের উপর যথাক্রমে DF এবং CE লম্ব আঁকা হলো।

△ADB এর ক্ষেত্রে:

• △ADB এর পরিসীমা = AD + DB + AB = ২৬ + ২৮ + ৩০ = ৮৪ সেমি
• অর্ধপরিসীমা (s) = পরিসীমা / ২ = ৮৪/২ = ৪২ সেমি

হিরনের সূত্রানুসারে, △ADB এর ক্ষেত্রফল:

ক্ষেত্রফল = √{s(s – a)(s – b)(s – c)} [যেখানে a, b, c ত্রিভুজের বাহুর দৈর্ঘ্য]

= √{৪২(৪২ – ৩০)(৪২ – ২৬)(৪২ – ২৮)}

= √{৪২ × ১২ × ১৬ × ১৪}

= √১১২৮৯৬

= ৩৩৬ বর্গ সেমি

আবার, △ADB এর ক্ষেত্রফল = (১/২) × AB × DF

= (১/২) × ৩০ × DF

= ১৫ × DF

সুতরাং, ১৫ × DF = ৩৩৬

বা, DF = ৩৩৬/১৫

বা, DF = ২২.৪ সেমি

যেহেতু DF এবং CE উভয়ই AB এর উপর লম্ব এবং AD = BC, তাই △ADF ≅ △BCE (RHS সর্বসমতা)।

সুতরাং, AF = BE = x (ধরি)

△ADF এ, পিথাগোরাসের উপপাদ্য অনুসারে:

AD² = AF² + DF²

বা, ২৬² = x² + (২২.৪)²

বা, ৬৭৬ = x² + ৫০১.৭৬

বা, x² = ৬৭৬ – ৫০১.৭৬

বা, x² = ১৭৪.২৪

বা, x = √১৭৪.২৪

বা, x ≈ ১৩.২ সেমি

সুতরাং, AF = BE ≈ ১৩.২ সেমি

এখন, AE = AB + BE = ৩০ + ১৩.২ = ৪৩.২ সেমি

△ACE এ, পিথাগোরাসের উপপাদ্য অনুসারে:

AC² = AE² + CE²

বা, AC² = (৪৩.২)² + (২২.৪)²

বা, AC² = ১৮৬৬.২৪ + ৫০১.৭৬

বা, AC² = ২৩৬৮

বা, AC = √২৩৬৮

বা, AC ≈ ৪৮.৬৬ সেমি

অতএব, ABCD সামন্তরিকের বৃহত্তম কর্ণের দৈর্ঘ্য প্রায় ৪৮.৬৬ সেমি।

১০. একটি রম্বসের পরিসীমা 180 সেমি এবং ক্ষুদ্রতম কর্ণটি 54 সেমি। এর অপর কর্ণ এবং ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

দেওয়া আছে:

• ABCD রম্বসের পরিসীমা = ১৮০ সেমি
• ক্ষুদ্রতম কর্ণ AC = ৫৪ সেমি
• কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করে।

নির্ণয় করতে হবে:

• বৃহত্তম কর্ণ BD এর দৈর্ঘ্য
• রম্বসের ক্ষেত্রফল

আমরা জানি, রম্বসের প্রত্যেক বাহু সমান।

সুতরাং,

• BC = পরিসীমা / ৪ = ১৮০/৪ = ৪৫ সেমি

আমরা জানি, রম্বসের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।

সুতরাং,

• OC = AC/২ = ৫৪/২ = ২৭ সেমি

আমরা জানি, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে।

সুতরাং, △BOC একটি সমকোণী ত্রিভুজ এবং ∠BOC = ৯০°।

পিথাগোরাসের উপপাদ্য অনুসারে,

BC² = OB² + OC²

বা, OB² = BC² – OC²

বা, OB² = ৪৫² – ২৭²

বা, OB² = ২০২৫ – ৭২৯

বা, OB² = ১২৯৬

বা, OB = √১২৯৬

বা, OB = ৩৬ সেমি

আমরা জানি, রম্বসের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।

সুতরাং,

• BD = ২ × OB = ২ × ৩৬ = ৭২ সেমি

অতএব, রম্বসের বৃহত্তম কর্ণের দৈর্ঘ্য ৭২ সেমি।

এখন, রম্বসের ক্ষেত্রফল = (১/২) × কর্ণদ্বয়ের গুণফল

= (১/২) × AC × BD

= (১/২) × ৫৪ × ৭২

= ১৯৪৪ বর্গ সেমি

অতএব, রম্বসের ক্ষেত্রফল ১৯৪৪ বর্গ সেমি।

১১. একটি ট্রাপিজিয়ামের সমান্তরাল বাহু দুইটির দৈর্ঘ্যের অন্তর 8 সেমি এবং এদের লম্ব দূরত্ব 24 সেমি। যদি ট্রাপিজিয়ামের ক্ষেত্রফল 312 বর্গ সেমি হয় তবে বাহু দুইটির দৈর্ঘ্য নির্ণয় কর।

সমাধানঃ

দেওয়া আছে:

• ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের মধ্যে পার্থক্য = ৮ সেমি
• সমান্তরাল বাহু দুইটির লম্ব দূরত্ব (উচ্চতা) h = ২৪ সেমি
• ট্রাপিজিয়ামের ক্ষেত্রফল = ৩১২ বর্গ সেমি

মনে করি,

• ট্রাপিজিয়ামের একটি সমান্তরাল বাহুর দৈর্ঘ্য = x সেমি
• ট্রাপিজিয়ামের অপর সমান্তরাল বাহুর দৈর্ঘ্য = (x + ৮) সেমি

আমরা জানি, ট্রাপিজিয়ামের ক্ষেত্রফল = (১/২) × (সমান্তরাল বাহুদ্বয়ের যোগফল) × উচ্চতা

সুতরাং,

ক্ষেত্রফল = (১/২) × [x + (x + ৮)] × ২৪

প্রশ্নমতে,

(১/২) × (২x + ৮) × ২৪ = ৩১২

বা, ১২(২x + ৮) = ৩১২

বা, ২৪x + ৯৬ = ৩১২

বা, ২৪x = ৩১২ – ৯৬

বা, ২৪x = ২১৬

বা, x = ২১৬/২৪

বা, x = ৯

অতএব,

• ট্রাপিজিয়ামের একটি সমান্তরাল বাহুর দৈর্ঘ্য = ৯ সেমি
• ট্রাপিজিয়ামের অপর সমান্তরাল বাহুর দৈর্ঘ্য = ৯ + ৮ = ১৭ সেমি

সুতরাং, ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য ৯ সেমি এবং ১৭ সেমি

১২. একটি ট্রাপিজিয়ামের সমান্তরাল বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 31 সেমি ও 11 সেমি এবং অপর বাহু দুইটির দৈর্ঘ্য যথাক্রমে 10 সেমি ও 12 সেমি। এর ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

দেওয়া আছে:

• ABCD ট্রাপিজিয়ামের সমান্তরাল বাহু AB = ৩১ সেমি
• CD = ১১ সেমি
• AD = ১০ সেমি
• BC = ১২ সেমি

অঙ্কন: AB থেকে CD এর সমান করে AE অংশ কেটে নিই এবং C থেকে AB এর উপর CF লম্ব আঁকি।

তাহলে, AE = CD = ১১ সেমি

সুতরাং, BE = AB – AE = ৩১ – ১১ = ২০ সেমি

এখন, △BCE এর ক্ষেত্রে:

• △BCE এর বাহুগুলির দৈর্ঘ্য: BE = ২০ সেমি, BC = ১২ সেমি, CE = AD = ১০ সেমি
• △BCE এর পরিসীমা = ২০ + ১২ + ১০ = ৪২ সেমি
• △BCE এর অর্ধপরিসীমা (s) = পরিসীমা / ২ = ৪২/২ = ২১ সেমি

হিরনের সূত্রানুসারে, △BCE এর ক্ষেত্রফল:

ক্ষেত্রফল = √{s(s – a)(s – b)(s – c)} [যেখানে a, b, c ত্রিভুজের বাহুর দৈর্ঘ্য]

= √{২১(২১ – ২০)(২১ – ১২)(২১ – ১০)}

= √{২১ × ১ × ৯ × ১১}

= √২০৭৯

≈ ৪৫.৫৮ বর্গ সেমি (প্রায়) (আপনি ৪৫.৫৯৬ লিখেছেন, যা প্রায় একই)

এখন, △BCE এর ক্ষেত্রফল = (১/২) × ভূমি × উচ্চতা = (১/২) × BE × CF

সুতরাং, (১/২) × ২০ × CF = ৪৫.৫৮

বা, ১০ × CF = ৪৫.৫৮

বা, CF = ৪৫.৫৮/১০

বা, CF ≈ ৪.৫৫৮ সেমি ≈ ৪.৫৬ সেমি (প্রায়) (আপনার মানটি সঠিক)

অতএব, ট্রাপিজিয়ামের উচ্চতা = CF ≈ ৪.৫৬ সেমি

সুতরাং, ট্রাপিজিয়ামের ক্ষেত্রফল = (১/২) × (সমান্তরাল বাহুদ্বয়ের যোগফল) × উচ্চতা

= (১/২) × (AB + CD) × CF

= (১/২) × (৩১ + ১১) × ৪.৫৬

= (১/২) × ৪২ × ৪.৫৬

= ২১ × ৪.৫৬

≈ ৯৫.৭৬ বর্গ সেমি (প্রায়) (আপনার ৯৫.৭৫ এসেছে, যা প্রায় একই)

অতএব, ট্রাপিজিয়ামের ক্ষেত্রফল প্রায় ৯৫.৭৬ বর্গ সেমি।

১৩. একটি সুষম অষ্টভুজের কেন্দ্র থেকে কৌণিক বিন্দুর দূরত্ব 1.5 মিটার হলে, এর ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ

মনে করি, ABCDEFGH একটি সুষম অষ্টভুজ এবং এর কেন্দ্র O। O থেকে শীর্ষবিন্দুগুলো যোগ করা হলো।

যেহেতু অষ্টভুজের ৮টি সমান বাহু এবং ৮টি সমান কোণ আছে, তাই কেন্দ্র O থেকে প্রতিটি শীর্ষবিন্দু যোগ করলে ৮টি সর্বসম ত্রিভুজ উৎপন্ন হবে।

∠AOB = ৩৬০°/৮ = ৪৫° (যেহেতু কেন্দ্রে ৩৬০° কোণ উৎপন্ন হয় এবং ৮টি সমান ভাগ হয়)

O কেন্দ্র থেকে শীর্ষবিন্দুগুলোর দূরত্ব, a = ১.৫ মিটার (অর্থাৎ, OA = OB = a = ১.৫ মিটার)

△AOB এর ক্ষেত্রফল নির্ণয়ের সূত্র: (১/২)a²sinθ, যেখানে a হলো দুটি বাহুর দৈর্ঘ্য এবং θ হলো তাদের মধ্যবর্তী কোণ।

∴ △AOB এর ক্ষেত্রফল = (১/২) × (১.৫)² × sin৪৫°

= (১/২) × ২.২৫ × (১/√২)

= ২.২৫ / (২√২)

= ২.২৫√২ / ৪ (লব ও হরকে √২ দিয়ে গুণ করে)

≈ ০.৭৯৫৪ বর্গমিটার (প্রায়) (আপনার ০.৭৯৫৫ প্রায় একই)

এখন, সুষম অষ্টভুজের ক্ষেত্রফল = ৮ × △AOB এর ক্ষেত্রফল

≈ ৮ × ০.৭৯৫৪

≈ ৬.৩৬৩২ বর্গমিটার (প্রায়) (আপনার ৬.৩৬৪ প্রায় একই)

অতএব, সুষম অষ্টভুজের ক্ষেত্রফল প্রায় ৬.৩৬৩২ বর্গমিটার।

প্র্যকটিসঃ

১৪. আয়তাকার একটি ফুলের বাগানের দৈর্ঘ্য 150 মিটার এবং প্রস্থ 100 মিটার। বাগানটিকে পরিচর্যা করার জন্য ঠিক মাঝ দিয়ে 3 মিটার চওড়া দৈর্ঘ্য ও প্রস্থ বরাবর রাস্তা আছে।

ক) উপরের তথ্যটি চিত্রের সাহায্যে সংক্ষিপ্ত বর্ণনা দাও।

সমাধানঃ

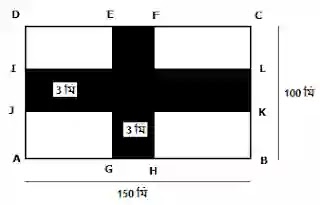
মনে করি, ABCD একটি আয়তাকার বাগান যার AB=DC=150 মি, CB=DA=100 মি। এবং বাগানের মাঝ বরাবর 3 মিটার চওড়া EFHG ও IJKL রাস্তা আছে।

খ) রাস্তার ক্ষেত্রফল নির্ণয় কর।

সমাধানঃ 

দেওয়া আছে:

• বাগানের দৈর্ঘ্য = ১৫০ মিটার
• বাগানের প্রস্থ = ১০০ মিটার

সুতরাং,

• বাগানের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ = ১৫০ × ১০০ = ১৫০০০ বর্গমিটার

আবার,

• রাস্তাবাদে বাগানের দৈর্ঘ্য = ১৫০ – ৩ = ১৪৭ মিটার
• রাস্তাবাদে বাগানের প্রস্থ = ১০০ মিটার (প্রস্থ একই থাকবে)

সুতরাং,

• রাস্তাবাদে বাগানের ক্ষেত্রফল = ১৪৭ × ১০০ = ১৪৭০০ বর্গমিটার

এখন, রাস্তার ক্ষেত্রফল = বাগানের ক্ষেত্রফল – রাস্তাবাদে বাগানের ক্ষেত্রফল

= ১৫০০০ – ১৪৭০০

= ৩০০ বর্গমিটার

অতএব, রাস্তার ক্ষেত্রফল ৩০০ বর্গমিটার।